インダクタはコンデンサとは正反対の特性を持っています。一方、コンデンサは電気にエネルギーを蓄えます 電界（2つのプレート間の電圧によって生成される）、インダクタは磁気にエネルギーを蓄積します フィールド（ワイヤを流れる電流によって生成されます）。したがって、コンデンサに蓄積されたエネルギーはその端子間で一定の電圧を維持しようとしますが、インダクタに蓄積されたエネルギーはその巻線を流れる一定の電流を維持しようとします。 このため、インダクタは電流の変化に対抗し、電圧の変化に対抗するコンデンサとは正反対に作用します。完全に放電されたインダクター（磁場なし）は、電流がゼロであり、電圧源に接続される

コンデンサは電界の形でエネルギーを蓄えるため、小さな二次電池のように機能する傾向があり、電気エネルギーを蓄えたり放出したりすることができます。完全に放電されたコンデンサは端子間でゼロボルトを維持し、充電されたコンデンサはバッテリーのように端子間で一定量の電圧を維持します。 コンデンサが他の電圧源との回路に配置されると、発電機に接続された結果として二次電池が充電されるのと同じように、コンデンサはそれらの電圧源からエネルギーを吸収します。端子電圧がゼロの完全に放電されたコンデンサは、電圧源に接続されると最初は短絡として機能し、充電を開始するときに最大電流を引き出します。 時間の経過とともに、コ

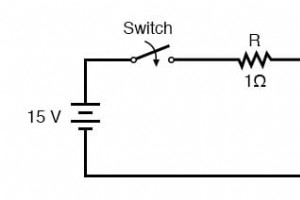
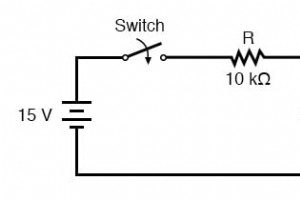
この章では、DC電圧の急激な変化（過渡と呼ばれる）に対するコンデンサとインダクタの応答について説明します。 電圧）、抵抗器と直列に配線されている場合。印加電圧に瞬時に反応する抵抗器とは異なり、コンデンサとインダクタは、エネルギーを吸収および放出するときに時間の経過とともに反応します。

インダクタには、すべての電気部品と同様に、信頼性と適切な回路動作のために尊重しなければならない制限があります。 インダクタンスに影響を与える要因 定格電流 インダクターはコイル状のワイヤーで構成されており、ワイヤーは抵抗と熱を放散する能力によって電流容量が制限されるため、インダクターに流れる最大電流に注意する必要があります。 等価回路 インダクタワイヤにはある程度の抵抗があり、回路設計の制約により、通常、インダクタを可能な限り最小の寸法に構築する必要があるため、「完璧な」インダクタなどはありません。インダクタコイルワイヤは通常、かなりの量の直列抵抗を示し、あるコイルターンから別のコ

インダクタが直列に接続されている場合、総インダクタンスは個々のインダクタのインダクタンスの合計です。これがなぜそうなのかを理解するために、次のことを考慮してください。インダクタンスの決定的な尺度は、インダクタを流れる電流変化の特定の速度でインダクタの両端に降下する電圧の量です。 インダクタが直列に接続されている場合（つまり、同じ電流を共有し、電流の変化率が同じである場合）、電流の変化の結果として低下する合計電圧は、各インダクタに加算され、より大きな合計電圧を作成します個々のインダクタのいずれか単独よりも。同じ電流変化率で電圧が高くなると、インダクタンスが大きくなります。 した

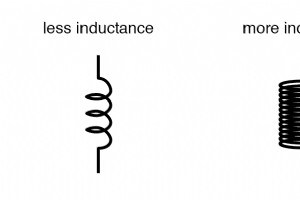
発生するインダクタンスの量を決定するインダクタ構造の4つの基本的な要因があります。これらの要因はすべて、特定の量の磁場力（インダクターのワイヤーコイルを流れる電流）に対して発生する磁場フラックスの量に影響を与えることにより、インダクタンスを決定します。 ワイヤラップの数、つまりコイルの「ターン」 他のすべての要因が等しい場合、コイル内のワイヤの巻き数が多いほど、インダクタンスが大きくなります。コイル内のワイヤの巻き数が少ないほど、インダクタンスが少なくなります。 説明： ワイヤの巻き数が多いということは、与えられた量のコイル電流に対して、コイルがより多くの磁場力（アンペアターンで測定！）を

インダクタには、導体のように安定した「抵抗」がありません。ただし、インダクタの電圧と電流の間には、次のように明確な数学的関係があります。 コンデンサの章からこの式の形式を認識する必要があります。これは、1つの変数（この場合はインダクターの電圧降下）を変化率に関連付けます。 別の変数（この場合、インダクタ電流）の。電圧（v）と電流変化率（di / dt）の両方が瞬時 ：つまり、特定の時点に関連して、小文字の「v」と「i」。 コンデンサの式と同様に、瞬時電圧を v として表すのが一般的です。 e ではなく 、しかし後者の指定を使用することは間違いではありません。現在の変化率（di

電子が導体を通って流れるときはいつでも、磁場がその導体の周りに発生します。この効果は電磁気学と呼ばれます 。 磁場は原子内の電子の整列に影響を与え、帯電した粒子間に力を発生させる電場と同様に、空間全体の原子間に物理的な力を発生させる可能性があります。電場と同様に、磁場は完全に空の空間を占め、離れた場所にある物質に影響を与える可能性があります。 フィールドフォースとフィールドフラックス フィールドには2つのメジャーがあります。フィールド force およびフィールド flux 。フィールド force フィールドが特定の距離にわたって及ぼす「プッシュ」の量です。フィールド flux

ワイヤーの2つのコイルを互いに近接させて、一方からの磁場が他方にリンクすると、結果として2番目のコイルに電圧が発生します。これは相互インダクタンスと呼ばれます ：あるコイルに印加された電圧が別のコイルに電圧を誘導したとき。 2つ以上のコイル間の相互インダクタンスの効果を生み出すように特別に設計されたデバイスは、トランスと呼ばれます。 。 上の写真に示されている装置は、2つの同心のワイヤーコイルを備えた一種の変圧器です。実際には相互インダクタンスの精密標準単位として意図されていますが、トランスの本質を説明するためにはそれで十分です。 2つのワイヤーコイルは色で区別できます。チ

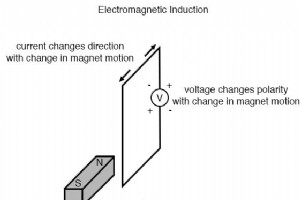
エルステッドの電磁気学の驚くべき発見は、より実用的なアプリケーションへの道を開きました。 電気の分野で、実用的な世代の鍵を私たちに与えてくれたのはマイケルファラデーでした。 電気の：電磁誘導 。ファラデーは、ワイヤーが強度が変化する垂直磁場フラックスにさらされた場合、そのワイヤーの長さ全体に電圧が発生することを発見しました。 強度が変化する磁場を作成する簡単な方法は、ワイヤーまたはワイヤーのコイルの隣に永久磁石を移動することです。 覚えておいてください： 磁場は、ワイヤーに垂直な強度で増加または減少する必要があります（これにより、磁束線が「横切る」ようになります。 コンダクター ）、そうで

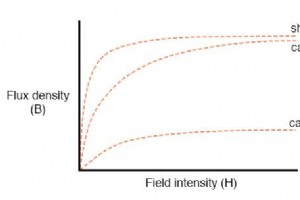
理解を深めるために、材料の透磁率の非線形性をグラフ化することができます。グラフの横軸に、電界力（mmf）を材料の長さで割った値に等しい電界強度（H）の量を配置します。縦軸には、全流束を材料の断面積で割った量に等しい流束密度（B）を配置します。 起磁力（mmf）と総磁束（Φ）の代わりに、電界強度（H）と磁束密度（B）の量を使用して、グラフの形状がテスト材料の物理的寸法に依存しないようにします。ここで私たちがやろうとしているのは、任意のの場の力と磁束の数学的関係を示すことです。 材料の特定の抵抗を説明するのと同じ精神で、特定の物質の塊 実際の抵抗の代わりにオーム-cmil / ftで オーム単位

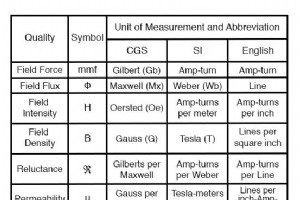
一般的な量（英語とメートル法）の2つの測定システムの負担が頭を混乱させる場合、これはあなたのための場所ではありません！磁性の科学における標準化の初期の欠如のために、私たちは磁性量の測定の3つ以上の完全なシステムに悩まされてきました。 まず、磁性に関連するさまざまな量に精通する必要があります。磁気システムでは、電気システムよりも処理する量がかなり多くあります。電気の場合、基本的な量は電圧（E）、電流（I）、抵抗（R）、および電力（P）です。 最初の3つはオームの法則（E =IR; I =E / R; R =E / I）によって相互に関連付けられ、電力はジュールの法則（P =IE; P =）に

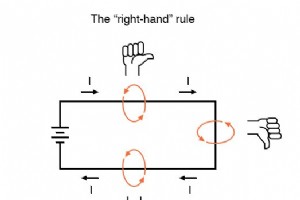
磁気と電気の関係の発見は、他の多くの科学的発見と同様に、ほとんど偶然に遭遇しました。デンマークの物理学者ハンスクリスチャンエルステッドは、1820年のある日可能性について講義していました。 電気と磁気は互いに関連しており、その過程で彼のクラス全体の前で実験することによってそれを決定的に示しました！ エルステッドは、磁気コンパスの上に吊るされた金属線に電流を流すことで、電流に応じてコンパスの針を明確に動かすことができました。クラスセッションの開始時に推測として始まったことは、最後に事実として確認されました。言うまでもなく、エルステッドは将来の授業のために講義ノートを改訂しなければなりませんでし

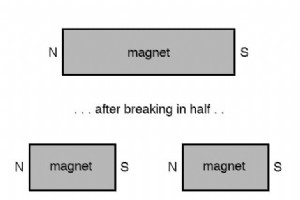
何世紀も前に、特定の種類の鉱物岩が金属鉄に引き付けられるという異常な特性を持っていることが発見されました。 ロードストーンと呼ばれる特定の鉱物 、またはマグネタイト は、非常に古い歴史的記録（ヨーロッパでは約2500年前、極東でははるかに早い時期）で好奇心の対象として言及されています。 後で、この珍しい岩の一部が自由に回転したままにすると（ひもまたは水中のフロートに吊るされた）、南北方向に向きを変える傾向があることがわかったため、ナビゲーションの助けとして採用されました。 。 1269年にPeterPeregrinusが行った科学的研究によると、鋼は、ロードストーンの「極」の1つにこすりつ

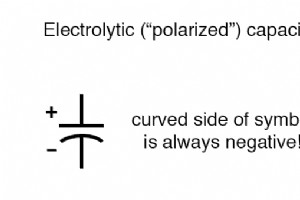
コンデンサには、すべての電気部品と同様に、信頼性と適切な回路動作のために尊重しなければならない制限があります。 コンデンサの動作電圧 動作電圧 ：コンデンサは、絶縁体（誘電体）によって分離された2つの導体にすぎないため、コンデンサの両端に許容される最大電圧に注意する必要があります。印加電圧が高すぎると、誘電体の「破壊」定格を超えて、コンデンサ内部が短絡する可能性があります。 コンデンサの極性 極性 ：一部のコンデンサは、一方の極性の印加電圧のみを許容し、もう一方の極性は許容しないように製造されています。これは、それらの構造によるものです。誘電体は、製造中にDC電圧によってプレートの1つに堆

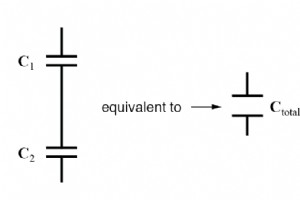
コンデンサが直列に接続されている場合、総静電容量は、直列コンデンサの個々の静電容量のいずれよりも小さくなります。 2つ以上のコンデンサが直列に接続されている場合、全体的な効果は、個々のコンデンサのプレート間隔の合計を持つ単一の（同等の）コンデンサの効果です。今見てきたように、他のすべての要因を変更せずにプレート間隔を大きくすると、静電容量が減少します。 したがって、総静電容量は、個々のコンデンサの静電容量のいずれよりも小さくなります。直列総静電容量の計算式は、並列抵抗の計算式と同じです。 コンデンサが並列に接続されている場合、総静電容量は個々のコンデンサの静電容量の合計になりま

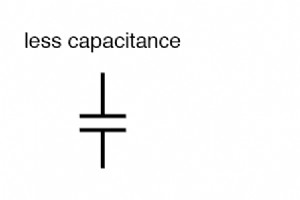
生成される静電容量の量を決定するコンデンサ構造の3つの基本的な要因があります。これらの要因はすべて、所定の電界力（2つのプレート間の電圧）に対して発生する電界フラックス（プレート間の電子の相対差）の量に影響を与えることにより、静電容量を決定します。 プレートエリア ：他のすべての要因が等しい場合、プレート面積が大きいほど静電容量が大きくなります。プレート面積が小さいほど静電容量が小さくなります。 説明： プレート面積が大きいほど、特定のフィールド力（プレート間の電圧）に対してより多くのフィールドフラックス（プレートに収集された電荷）が発生します。 プレート間隔 ：他のすべての要因が

コンデンサには、導体のように安定した「抵抗」がありません。ただし、コンデンサの電圧と電流の間には、次のように明確な数学的関係があります。 小文字の「i」は瞬時を表します 電流。特定の時点での電流の量を意味します。これは、不特定の期間にわたる定電流または平均電流（大文字の「I」）とは対照的です。 「dv / dt」という表現は、計算から借用したもので、時間の経過に伴う電圧の瞬間的な変化率、または特定の時点での電圧の変化率（1秒あたりの電圧の増加または減少）を意味します。瞬時電流が参照される時間。なんらかの理由で、 v という文字 通常、文字 e ではなく、瞬時電圧を表すために使用されます

はじめに 分離された2つの導体間に電圧が存在する場合は常に、それらの導体間の空間内に電界が存在します。基本的な電子機器では、電圧、電流、抵抗が回路に関係する相互作用を研究します。回路は、電子が移動する可能性のある導電経路です。ただし、フィールドについて話すときは、空きスペース全体に広がる可能性のある相互作用を扱っています。 確かに、「フィールド」の概念はやや抽象的なものです。少なくとも電流では、電子と呼ばれる小さな粒子が導体内の原子核間を移動することを想像するのはそれほど難しくありませんが、「フィールド」には質量すらなく、物質内に存在する必要はまったくありません。 。 その抽象的な性質に

絶縁材料の原子は非常に緊密に結合した電子を持っており、自由な電子の流れに非常によく抵抗します。ただし、絶縁体は無期限の電圧に耐えることができません。十分な電圧が印加されている場合、任意 絶縁材料は最終的に電気的な「圧力」に屈し、電流が流れます。ただし、電流が印加電圧に線形に比例する導体の状況とは異なり（固定抵抗が与えられた場合）、絶縁体を流れる電流は完全に非線形です。特定のしきい値を下回る電圧の場合、実質的に電流は流れませんが、印加電圧がそのしきい値電圧（ ブレークダウン電圧として知られています） または 絶縁耐力 ）、流れが殺到するでしょう。 絶縁耐力 絶縁破壊を引き起こすのに必要