








カルノーについて学ぶ理由 マップ?ブール代数のようなカルノー図は、デジタルロジックに適用できる簡略化ツールです。デジタルロジックのブール単純化の例については、ブール代数の章の「有毒廃棄物焼却炉」を参照してください。 カルノー図は、ほとんどの場合、ロジックをより速く、より簡単に簡素化します。 ブール単純化は、実際には、2つ以下のブール変数を含むタスクのカルノー図よりも高速です。それでも3つの変数でかなり使用できますが、少し遅くなります。 4つの入力変数では、ブール代数は面倒になります。 カルノー図はより速く、より簡単です。カルノー図は、最大6つの入力変数に対して適切に機能し、最大8つの変
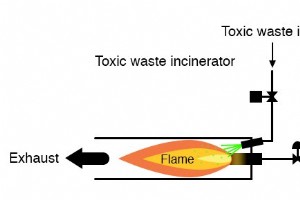
デジタル回路を設計する際、設計者は回路が何をすべきかを説明する真理値表から始めることがよくあります。 設計タスクは主に、真理値表に記載されている機能を実行する回路のタイプを決定することです。 真理値表を見て、タスクに必要な論理ゲートまたはリレー論理回路をすぐに想像する自然な能力を持っている人もいますが、残りの人が利用できる手順のテクニックがあります。 ここで、ブール代数は最も劇的な方法でその有用性を証明しています。 この手続き型の方法を説明するために、現実的な設計の問題から始める必要があります。 有毒廃棄物焼却炉の火炎検出回路を設計するタスクが与えられたとします。 火の強烈な熱
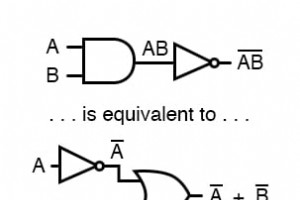
DeMorganという名前の数学者は、ブール代数のグループ補完に関する2つの重要なルールを開発しました。 グループ 補完、私は複数の変数の上の長いバーで表される用語のグループの補完を指します。 論理ゲートの章から、ゲートへのすべての入力を反転すると、そのゲートの基本的な機能がANDからORに、またはその逆に反転し、出力も反転することを思い出してください。 したがって、すべての入力が反転されたORゲート(負のORゲート)はNANDゲートと同じように動作し、すべての入力が反転されたANDゲート(負のANDゲート)はNORゲートと同じように動作します。 ド・モルガンの定理は、「逆方向」の形

XORゲートとは何ですか? ブール演算のセットから著しく欠落している要素の1つは、排他的論理和の要素であり、多くの場合XORとして表されます。 OR関数はブール加算、AND関数はブール乗算、NOT関数(インバーター)はブール補完と同等ですが、排他的論理和と同等の直接ブール関数はありません。 ただし、これは、人々がこの論理ゲートを表すシンボルを開発することを妨げるものではありません。 この論理ゲート記号は、ブール式ではめったに使用されません。これは、加算、乗算、および補完を含む単純化のID、法則、および規則が適用されないためです。 ただし、前の章で示したように、ORとAN
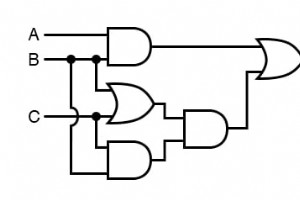
簡略化が必要な半導体ゲート回路から始めましょう。 「A」、「B」、および「C」の入力信号は、スイッチ、センサー、またはおそらく他のゲート回路から提供されると想定されています。 これらの信号がどこで発生するかは、ゲート削減のタスクでは問題になりません。 回路を単純化するブール式の書き方 単純化の最初のステップは、この回路のブール式を作成することである必要があります。 このタスクは、各ゲートのそれぞれの入力信号に対応するサブ式を各ゲートの出力に書き込むことから始めれば、段階的に簡単に実行できます。 ORゲートはブール加算に相当し、ANDゲートはブール乗算に相当することに注意
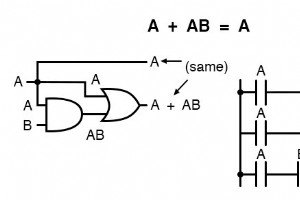
ブール代数は、論理回路の単純化に最も実用的です。 論理回路の関数をシンボリック(ブール)形式に変換し、結果の方程式に特定の代数規則を適用して項や算術演算の数を減らすと、簡略化された方程式は、実行する論理回路の回路形式に変換されます。より少ないコンポーネントで同じ機能。 より少ないコンポーネントで同等の機能を実現できれば、信頼性が向上し、製造コストが削減されます。 この目的のために、このセクションでは、式を最も単純な形式に変換するために使用するブール代数の規則がいくつかあります。 この章ですでに確認した恒等式とプロパティは、ブール代数の単純化に非常に役立ち、ほとんどの場合、「通常の」代数
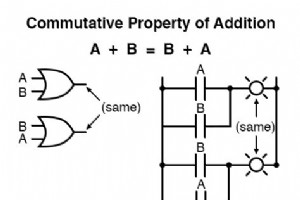
「プロパティ」または「法則」と呼ばれる別のタイプの数学的恒等式は、異なる変数が数のシステムで互いにどのように関連するかを説明します。 可換性 これらのプロパティの1つは、c ommutativeプロパティとして知られています。 、そしてそれは足し算と掛け算に等しく適用されます。 本質的に、可換性は、式の真理を変えることなく、加算または乗算される変数の順序を逆にすることができることを示しています。 結合プロパティ 加算と乗算の可換性に加えて、結合法則があります。 、加算と乗算にも同様に適用できます。 このプロパティは、方程式の真理を変更することなく、追加または
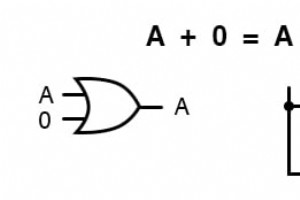
数学では、アイデンティティ 1つまたは複数の変数のすべての可能な値に当てはまるステートメントです。 x + 0 =xの代数的単位元は、何でも (x)ゼロに追加 「何でも」の値に関係なく、元の「何でも」に等しい 」(x)は可能性があります。 通常の代数と同様に、ブール代数には、ブール変数の2価の状態に基づいた独自のIDがあります。 加法単位元 ゼロの追加 最初のブールIDは、すべての合計です。 およびゼロ 元の「何でも」と同じです 。」 このアイデンティティは、実数の代数に相当するものと同じです: A の値に関係なく 、出力は常に同じになります: A =1 の場合

数値を足し合わせてブール代数の探索を始めましょう: 最初の3つの合計は、初歩的な足し算に精通している人には完全に理にかなっています。 ただし、最後の合計は、数学の基本原則に反しているように見えるため、デジタル電子機器の他のどの単一のステートメントよりも混乱の原因となる可能性があります。 まあ、それは実数の加算の原則と矛盾しますが、ブール数の場合は矛盾しません。 ブール代数の世界では、任意の量と任意の算術演算に対して可能な値は1または0の2つだけであることに注意してください。 ブール値の範囲内に「2」のようなものはありません。 「1+ 1」の合計は確かに0ではないため、消

数学的規則は、扱われる特定の数値に課す定義上の制限に基づいています。 1 + 1 =2または3+ 4 =7と言うときは、整数の量を使用していることを意味します。これは、初等教育で数えることを学んだのと同じ種類の数です。 ほとんどの人が自明の算術規則であると想定していること(常に、あらゆる目的で有効)は、実際には、数値を定義する内容によって異なります。 たとえば、AC回路の数量を計算する場合、DC回路の分析で非常に役立つ「実数」の数量は、AC数量を表すタスクには不十分であることがわかります。 直列に接続すると電圧が加算されることはわかっていますが、3ボルトのAC電源を4ボルトのAC電源と

ソリッドステート論理回路が登場する前は、論理制御システムは電気機械式リレーのみを中心に設計および構築されていました。リレーは現代の設計では時代遅れにはなりませんが、ロジックレベルの制御デバイスとしての以前の役割の多くに置き換えられ、大電流および/または高電圧スイッチングを必要とするアプリケーションに最も頻繁に追いやられています。 「オン/オフ」制御を必要とするシステムとプロセスは、現代の商工業に豊富にありますが、そのような制御システムが電気機械式リレーまたはディスクリート論理ゲートのいずれかから構築されることはめったにありません。代わりに、デジタルコンピュータがニーズを満たします。これはプロ
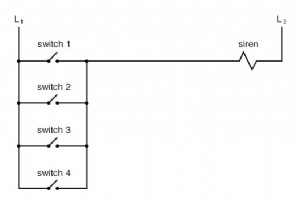
電気機械式リレーまたはソリッドステートゲートで構成されているかどうかにかかわらず、論理回路は、同じ機能を実行するためにさまざまな方法で構築できます。 通常、複雑な論理回路を設計するための「正しい」方法はありませんが、通常、他の方法よりも優れた方法があります。 制御システムでは、安全性が重要な設計上の優先事項です(または少なくともそうあるべきです)。 タスクを実行するためにデジタル制御回路を設計できる方法が複数あり、そのうちの1つが他の方法よりも安全性に一定の利点を持っている場合は、その設計を選択するのが適切です。 制御システムでのリレーロジックの実装 単純なシステムを見て、リレーロ

前のセクションのモーター制御回路に取り付けられたインターロック接点は正常に機能しますが、モーターは各押しボタンスイッチが押されている間のみ動作します。 オペレーターが制御スイッチから手を離した後もモーターを動かし続けたい場合は、いくつかの異なる方法で回路を変更できます。プッシュボタンスイッチをトグルスイッチに置き換えるか、いずれかのスイッチを1回瞬間的に作動させるだけで、制御回路を「ラッチ」するためのリレーロジックをさらに追加できます。 2番目のアプローチは業界で一般的に使用されているため、どのように実装されているかを見てみましょう。 「進む」押しボタンが作動すると、M
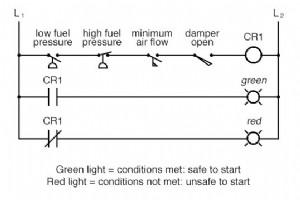
スイッチとリレーロジックの実際のアプリケーションは、機器の起動を許可する前にいくつかのプロセス条件を満たさなければならない制御システムです。 この良い例は、大型燃焼炉のバーナー制御です。 大型炉のバーナーを安全に始動するために、制御システムは、高低燃料圧力、空気ファン流量チェック、排気スタックダンパー位置、アクセスドア位置などのいくつかのプロセススイッチからの「許可」を要求します。 各プロセス条件は許容と呼ばれます 、および各許容スイッチ接点は直列に配線されているため、いずれかが危険な状態を検出すると、回路が開きます。 すべての許容条件が満たされている場合、CR 1
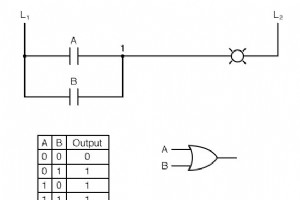
複数の接点を使用して、架空のランプ回路の単純な論理関数を構築し、元の「ラダー」にラングを追加することで、これらの回路を非常に簡単かつ理解できるように文書化できます。 スイッチとランプのステータスに標準のバイナリ表記を使用する場合(0は非作動または非通電、1は作動または通電)、真理値表を作成して、ロジックがどのように機能するかを示すことができます。 これで、接点Aまたは接点Bのいずれかが作動すると、ランプが点灯します。これは、ランプに通電するために必要なのは、ワイヤL 1 からの電流の経路が少なくとも1つあることだけだからです。 配線1に。 私たちが持っているのは、接点とラ
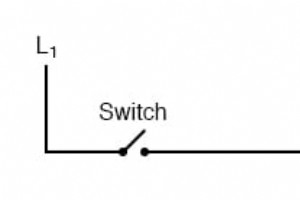
ラダーダイアグラムは、産業用制御ロジックシステムを文書化するために一般的に使用される特殊な回路図です。 これらは、2つの垂直レール(供給電力)と、表現する制御回路の数と同じ数の「ラング」(水平線)を備えたはしごに似ているため、「はしご」図と呼ばれます。 ハンドスイッチで制御されるランプを示す簡単なラダー図を描きたい場合は、次のようになります。 「L 1 」および「L 2 」の指定は、特に明記されていない限り、120VAC電源の2つの極を指します。 L 1 は「ホット」コンダクターであり、L 2 は接地された(「中性」)導体です。 これらの指定は、物事を混乱
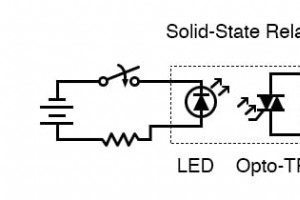
電気機械式リレーの制限 電気機械式リレーは用途が広いので、多くの制限があります。最新の半導体デバイスと比較して、構築に費用がかかり、接触サイクルの寿命が限られており、多くのスペースを占有し、ゆっくりと切り替える可能性があります。 これらの制限は、大電力コンタクタリレーに特に当てはまります。 ソリッドステートリレー これらの制限に対処するために、多くのリレーメーカーは、制御された電力を切り替えるために機械的接点の代わりにSCR、トライアック、またはトランジスタ出力を使用する「ソリッドステート」リレーを提供しています。出力デバイス(SCR、トライアック、またはトランジスタ)は、リレー内のLE

特殊なタイプのリレーは、異常な状態が発生した場合に回路ブレーカーを開くために、電流、電圧、周波数、またはその他のタイプの電力測定値を発電源または負荷のいずれかから監視するものです。 。これらのリレーは、電力業界では保護リレーと呼ばれています。 サーキットブレーカとしての電気機械式リレー 大量の電力のオンとオフを切り替えるために使用される回路ブレーカーは、実際には電気機械式リレーです。住宅用および商業用に見られるサーキットブレーカは、過電流によって熱くなりすぎると曲がる内部のバイメタルストリップによってトリップ(開く)するタイミングを決定しますが、大型の産業用サーキットブレーカは、外部デバイス

時間遅延リレーとは何ですか? 一部のリレーは、アーマチュアに取り付けられた一種の「ショックアブソーバー」メカニズムで構成されており、コイルがオンまたはオフのときに即座に完全に動くのを防ぎます。この追加により、リレーに time-delay のプロパティが与えられます。 作動。 時間遅延リレーは、コイルの通電、非通電、またはその両方で電機子の動きを遅らせるように構築できます。時間遅延リレーの接点は、通常開または通常閉のいずれかとして指定するだけでなく、遅延が次の方向に動作するかどうかを指定する必要があります。閉じるか開く方向に。 以下は、時間遅延リレー接点の4つの基本的なタイプの説明です。
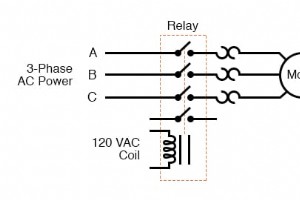
コンタクタのすべて リレーを使用して接点を介して大量の電力を切り替える場合、リレーは特別な名前で示されます:コンタクタ 。コンタクタには通常複数の接点があり、それらの接点は通常(常にではありませんが)通常は開いているため、コイルの電源が切られると負荷への電力が遮断されます。 おそらく、接触器の最も一般的な産業用途は、電気モーターの制御です。 上の3つの接点は、入力される3相AC電源のそれぞれの相を切り替えます。通常、1馬力以上のモーターの場合は少なくとも480ボルトです。最も低い接点は「補助」接点であり、大きなモーター電源接点よりも電流定格がはるかに低くなっていますが、電源
産業技術