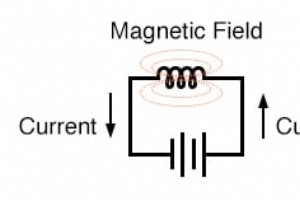
電気と磁気 導体を流れる電流は、導体を取り囲む磁力線を生成します。その導体がコイル状に巻かれている場合、生成される磁場はコイルの長さに沿って方向付けられます。電流が大きいほど、磁場の強さが大きくなり、他のすべての要因は等しくなります。 インダクタと磁場 インダクタは、この磁場に蓄積されたエネルギーのために電流の変化に反応します。共通の鉄心の周りに2つのインダクターコイルから変圧器を構築する場合、このフィールドを使用して、一方のコイルからもう一方のコイルにエネルギーを転送します。 ただし、インダクタやトランスで見たアプリケーションよりも、電磁界のより単純で直接的な使用法があり

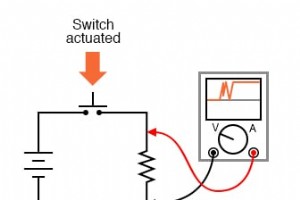
スイッチが作動し、作動力の下で接点が互いに接触すると、それらは単一の鮮明な瞬間に連続性を確立することになっています。 ただし、残念ながら、スイッチはこの目標を正確に達成していません。可動接点の質量と、メカニズムおよび/または接点材料に固有の弾性により、接点は、完全に静止して途切れのない接触を提供する前に、数ミリ秒の閉鎖時に「跳ね返り」ます。 多くのアプリケーションでは、スイッチのバウンスは重要ではありません。白熱灯を制御するスイッチが作動するたびに数サイクル「バウンス」しても、ほとんど問題になりません。ランプのウォームアップ時間はバウンス期間を大幅に超えるため、ランプの動作に異常は発生しま

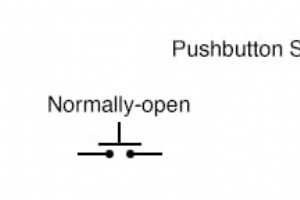
あらゆる種類のスイッチ接点は、作動時に接点が「閉じる」（導通を確立する）ように、または作動すると「開く」（導通を中断する）ように設計できます。 ばねが戻るメカニズムを備えたスイッチの場合、力を加えずにばねが元に戻す方向を通常と呼びます。 位置。 したがって、この位置で開いている接点は、通常開いていると呼ばれます。 この位置で閉じている接点は、通常閉じていると呼ばれます。 。 「通常の」プロセス切り替え条件 プロセススイッチの場合、通常の位置または状態は、プロセスの影響がないときにスイッチが置かれている位置です。 プロセススイッチの通常の状態を把握する簡単な方法は、スイッチがストレー

スイッチは、2つの導体を制御された方法で相互に接触させる任意のメカニズムで構築できます。 これは、レバーを動かすか、2つの金属ストリップを直接押して接触させることで、2本の銅線を互いに接触させるのと同じくらい簡単です。 ただし、優れたスイッチ設計は頑丈で信頼性が高く、感電の可能性をオペレーターに提示しないようにする必要があります。したがって、産業用スイッチの設計がこれほど粗雑になることはめったにありません。 電気接続を確立および切断するために使用されるスイッチの導電性部品は、接点と呼ばれます。 。 接点は通常、銀または銀カドミウム合金でできており、その導電特性は表面の腐食や酸化によって

この本シリーズのこのような後期段階で電気スイッチの基本的なトピックを取り上げるのは奇妙に思えるかもしれませんが、次の章では、ソリッドステートゲート回路ではなく機械式スイッチ接点に基づくデジタル技術の古い領域を探求しているためです。 、およびスイッチの種類を完全に理解する必要があります。 ソリッドステート論理ゲートについて学ぶと同時にスイッチベースの回路の機能を学ぶことで、両方のトピックを理解しやすくなり、デジタル論理回路の背後にある数学であるブール代数の学習体験を向上させるための準備が整います。 電気スイッチとは何ですか？ 電気スイッチは、回路内の電子の流れを遮断するために使用されるデバ

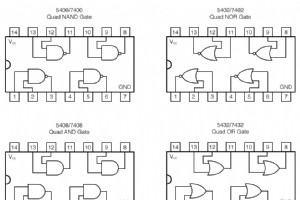
デジタル論理ゲート回路は集積回路として製造されています。すべての構成トランジスタと抵抗は、単一の半導体材料上に構築されています。少数のゲートを使用するエンジニア、技術者、または趣味の人は、必要なものがDIP（デュアルインラインパッケージ）ハウジングに封入されていることに気付くでしょう。 DIPで囲まれた集積回路は、標準の回路基板レイアウトの互換性のために、互いに0.100インチ間隔で配置された偶数のピンで利用できます。ピン数8、14、16、18、および24は、DIP「チップ」で一般的です。 部品番号 これらのDIPパッケージに付けられた部品番号は、囲まれているゲートのタイプと数を指定します

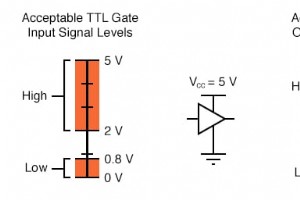
論理ゲートの入力電圧 論理ゲート回路は、可変電圧で表される「高」（1）と「低」（0）の2種類の信号のみを入出力するように設計されています。「高」状態の場合は全電源電圧、 「低」状態。完璧な世界では、すべての論理回路信号はこれらの極端な電圧限界に存在し、それらから逸脱することはありません（つまり、「高」の場合は全電圧未満、「低」の場合はゼロより高い電圧）。 ただし、実際には、トランジスタ回路の漂遊電圧降下により、論理信号電圧レベルがこれらの完全な制限に達することはめったにありません。したがって、ゲート回路が 完全な供給電圧とゼロ。 TTLゲート入力の耐電圧 TTLゲートは、5ボルト

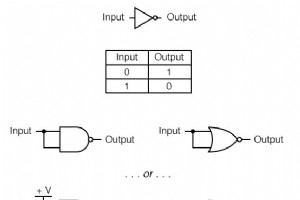
NANDゲートとNORゲートには特別な特性があります。それらはユニバーサルです。つまり、十分な数のゲートがあれば、どちらのタイプのゲートも他のタイプのゲートの動作を模倣できます。 たとえば、3つの相互接続されたNANDゲートを使用して、OR機能を示す回路を構築することができます。シングルゲートタイプが他のゲートタイプを模倣できる能力は、NANDとNORだけが享受できるものです。実際、デジタル制御システムは、NANDゲートまたはNORゲートのいずれかを中心に設計されており、必要なすべての論理機能は、相互接続されたNANDまたはNORのコレクションから派生しています。 この特性の証拠として、こ

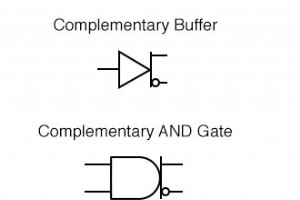
補完出力ゲート 反転出力と非反転出力の両方を提供する論理ゲートが望ましい場合があります。たとえば、バッファとインバータの両方であり、機能ごとに個別の出力端子を備えた単一入力ゲート。 または、単一の回路でANDとNANDの両方の機能を提供する2入力ゲート。このようなゲートは実際に存在し、相補出力ゲートと呼ばれます。 。 このようなゲートの一般的な記号は、バーとそこから突き出た2本の出力ラインを備えた基本的なゲート図です。次の図に、相補ゲートシンボルの配列を示します。 補完ゲートの使用 補完ゲートは、標準ゲートと追加のインバーターを使用して反転出力と非反転出力の両方を提供す

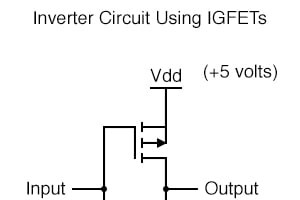
これまで、トランジスタロジック回路の分析は TTL に限定されていました。 設計パラダイム。これにより、バイポーラトランジスタが使用され、フローティング入力の一般的な戦略は「高」（V cc に接続）と同等になります。 ）入力（およびそれに対応して、「オープンコレクタ」出力ステージの許容値）は維持されます。ただし、これが論理ゲートを構築できる唯一の方法ではありません。 電界効果トランジスタ 電界効果トランジスタ、特に絶縁ゲートの種類は、ゲート回路の設計に使用できます。 IGFETは、電流制御デバイスではなく電圧制御デバイスであるため、非常に単純な回路設計を可能にする傾向があります。たとえば、

TTL回路解析 次のTTL回路を調べて、その動作を分析してみましょう。 トランジスタQ1とQ2はどちらも、他のすべてのTTL回路のトランジスタQ1で見たのと同じ方法で配置されています。 Q1とQ2は、増幅器として機能するのではなく、2ダイオードの「ステアリング」ネットワークとして使用されています。説明のために、Q1とQ2をダイオードセットに置き換える場合があります。 入力Aがフローティングのままになっている（またはVccに接続されている）場合、電流はトランジスタQ3のベースを流れ、トランジスタQ3を飽和させます。入力Aが接地されている場合、その電流は「Q1」の

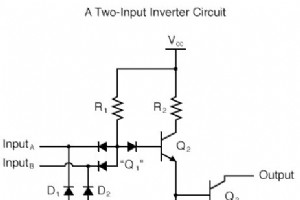
基本的なオープンコレクターインバーター回路を変更し、最初の入力端子と同じように2番目の入力端子を追加したとします。 この回路図は実際の回路を示していますが、「2入力インバータ」とは呼ばれていません。分析を通じて、この回路の論理関数が何であるか、それに対応してそれが何として指定されるべきかを発見します。 インバーターとバッファーの場合と同様に、「Q1」とマークされた「ステアリング」ダイオードクラスターは、増幅能力で使用されていなくても、実際にはトランジスタのように形成されます。残念ながら、単純なNPNトランジスタ構造では、 3つをシミュレートするには不十分です。 このダイ

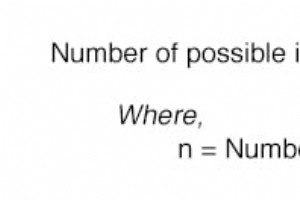
論理ゲートの使用 インバーターとバッファーは、単一入力ゲート回路の可能性を使い果たします。単一の論理信号で、それをバッファリングまたは反転する以外に何ができるでしょうか？より多くの論理ゲートの可能性を探求するには、回路に入力端子を追加する必要があります。 論理ゲートに入力端子を追加すると、入力状態の可能性が増えます。インバータやバッファなどの単一入力ゲートでは、入力状態は2つしかありません。入力が「ハイ」（1）または「ロー」（0）のいずれかです。 この章で前述したように、2つの入力ゲートには 4つあります。 可能性（00、01、10、および11）。 3入力ゲートには 8 入力状態の可能

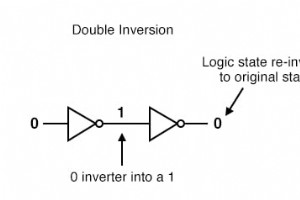
1つの出力が別の入力に供給されるように2つのインバータゲートを接続すると、2つの反転関数は互いに「キャンセル」され、入力から最終出力への反転が発生しなくなります。 これは無意味に思えるかもしれませんが、実用的なアプリケーションがあります。ゲート回路は信号増幅器であることを忘れないでください 、実行する可能性のある論理機能に関係なく。 弱い信号源（負荷にあまり多くの電流を供給またはシンクすることができないもの）は、前の図に示されているペアのような2つのインバーターによってブーストされる場合があります。ロジックレベルは変更されていませんが、必要に応じて、最終的なインバータの完全

前に示したシングルトランジスタインバータ回路は、実際には粗すぎてゲートとして実用化できません。実際のインバータ回路には、電圧ゲインを最大化するための複数のトランジスタ（最終出力トランジスタが完全にカットオフまたは完全に飽和するようにするため）と、偶発的な損傷の可能性を減らすように設計されたその他のコンポーネントが含まれています。 実用的なインバータの概略図 ここに示されているのは、実際のインバータ回路の概略図であり、効率的で信頼性の高い動作に必要なすべてのコンポーネントが含まれています。 この回路は、抵抗、ダイオード、バイポーラトランジスタのみで構成されています。バイポーラの代わ

2進数の記数法は興味深い数学的抽象化ですが、電子機器への実際の適用はまだ見ていません。この章では、それだけに専念します。バイナリビットの概念を回路に実際に適用します。 2進数をデジタル電子機器のアプリケーションにとって非常に重要にしているのは、ビットを物理的に簡単に表現できることです。バイナリビットは、0または1の2つの異なる値のいずれかしか持つことができないため、2つの飽和状態を切り替えることができる任意の物理媒体を使用してビットを表すことができます。 その結果、2進ビットを表すことができる物理システムは、数値を表すことができ、潜在的にそれらの数値を操作することができます。これがデジタル

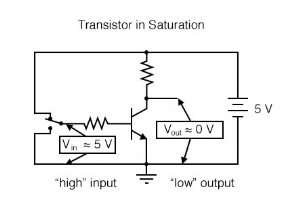
電子機器で2進記数法を学び、使用する唯一の理由は、デジタル形式で数値を表現および処理する回路を設計、構築、およびトラブルシューティングする方法を理解することです。 バイナリビット数の2価（2値）システムは、「オン」および「オフ」トランジスタ状態（それぞれ飽和およびカットオフ）による表現に非常に適しているため、この原理を利用して回路を設計および構築することは理にかなっています。バイナリ計算。 2進数を表す回路を構築する場合、必要な数のビットを表すのに十分なトランジスタ回路を割り当てる必要があります。つまり、デジタル回路を設計する際には、最初に表現できるビット数（最大）を決定する必要があります

符号付き2進数の注意点の1つは、オーバーフローの場合です。この場合、加算または減算の問題に対する答えが、割り当てられたビット数で表すことができる大きさを超えます。符号ビットの場所は問題の最初から固定されていることを忘れないでください。 最後の例の問題では、5つの2進ビットを使用して数値の大きさを表し、左端（6番目）のビットを負の重み（符号）ビットとして使用しました。大きさを表す5ビットでは、2 5 の表現範囲があります。 、または0から最大までの32の整数ステップ。 これは、+ 31 10 までの数値を表すことができることを意味します （011111 2 ）、または最低-32 1

10進数に適合した標準的な手法を使用して、ある2進数を別の2進数から減算できます（各ビットペアの右から左への減算、必要に応じてビットから左への「借用」）。ただし、すでにおなじみの（そしてより簡単な）2進加算の手法を利用して減算できるのであれば、それはより良いでしょう。 先ほど学習したように、「2の補数」法と負の場所の重みビットを使用して、負の2進数を表すことができます。ここでは、これらの負の2進数を使用して、加算によって減算します。 問題の例を次に示します。 減算：7 10 -5 10 同等の追加：7 10 +（-5 10 ）。 7と負の5を2進数（2の補数）形

足し算が簡単にできるので、数字の1つを負にするだけで、同じ手法で減算の演算を実行できます。たとえば、7-5の減算問題は、加算問題7 +（-5）と本質的に同じです。 正の数を2進数で表す方法はすでにわかっているので、今知っておく必要があるのは、負の数を表す方法だけで、減算できるようになります。 通常、負の10進数は、上記の例のように、最上位桁のすぐ左にマイナス記号-5を付けて表します。ただし、2進表記を使用する目的は、電圧でビット値を表すことができるオン/オフ回路を構築することです（2つの代替値：「高」または「低」のいずれか）。 このコンテキストでは、これらの回路はオンまたはオフ（2つ