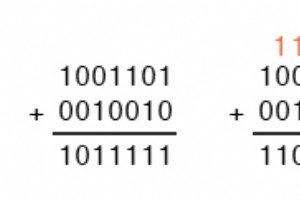
バイナリ加算のルール 2進数の加算は非常に単純な作業であり、10進数の長い加算と非常によく似ています。 10進数の場合と同様に、ビット（数字）を1列ずつ追加するか、右から左に一度に重みを付けます。 10進数の加算とは異なり、2進ビットの加算の規則について覚えておくべきことはほとんどありません。 0 + 0 =0 1 + 0 =1 0 + 1 =1 1 + 1 =10 1 + 1 + 1 =11 10進数の加算と同様に、1つの列の合計が2ビット（2桁）の数値の場合、最下位の数字は合計の一部として書き込まれ、最上位の数字は次の左側の列に「運ばれ」ます。 。次の例を検討してください

数値を表すために使用される記数法のタイプは、算術関数（加算、減算、乗算、除算、根、累乗、または対数）の結果に影響を与えないことを理解することが不可欠です。 数は数です。数は数です。 1、1、および2をどのように象徴するかに関係なく、1 + 1は常に2に等しくなります（実数を扱っている限り）。 10進数形式の素数は、2進数形式、8進数、または16進数で表示されている場合でも素数です。円周率は、その値を表すために使用する記号に関係なく、円の円周と直径の比率です。 数学の本質的な機能と相互関係は、量を表すために選択する可能性のある特定の記号体系の影響を受けません。数と記数法のこの区別は、理解する

8進数と16進数の記数法には、2進数の倍数の基数（基数2）があるため、16進数または8進数と2進数の間の変換は非常に簡単です。 また、10進法に精通しているため、2進数、8進数、または16進数を10進数形式に変換するのは比較的簡単です（暗号値と桁の重みの積を合計するだけです）。 ただし、10進数からこれらの「奇妙な」記数法への変換は別の問題です。 トライアルアンドフィット方式 おそらく最も理にかなっている方法は、「試行と適合」法です。この方法では、10進形式で表される目的の値に、2進、8進、または16進表記を「適合」させようとします。 たとえば、87の10進値を2進形式で表現したい

8進数および16進数の記数法の主な目的は、デジタル電子機器での2進数の「省略形」表現ですが、これらのシステムのいずれかから10進数形式に変換する必要がある場合があります。 もちろん、16進数または8進数の形式を2進数に変換してから、2進数から10進数に変換することもできます。これは、両方の方法をすでに知っているためですが、直接変換することもできます。 8進数は8進数の記数法であるため、各場所の重みの値は、隣接する場所とは8倍異なります。 たとえば、8進数の245.37は、次のように場所の値に分解できます。 各8進数の桁の重みにそれぞれの暗号乗数を掛けたものの10進数値は、

2進数は、10進法の経済性と比較して比較的小さな数を表すために非常に多くのビットを必要とするため、デジタル電子回路内の数値状態を分析することは退屈な作業になる可能性があります。 コンピューターに何をすべきかを指示する数字コードのシーケンスを設計するコンピュータープログラマーは、デジタル回路の「母国語」である1と0の長い文字列だけで作業することを余儀なくされた場合、非常に困難な作業になります。 人間のエンジニア、技術者、プログラマーがデジタル世界のこの言語を「話す」ことを容易にするために、バイナリへの変換とバイナリからの変換が非常に簡単な場所加重数え上げの他のシステムが作成されました。 そ

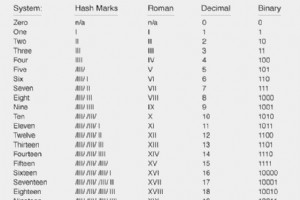
ハッシュマーク、ローマ数字、10進数、2進数の、4種類の記数法を使用して0から20まで数えましょう。 ハッシュマークもローマ数字も、大きな数を象徴するのに非常に実用的ではありません。明らかに、10進数や2進数などの場所加重システムは、タスクに対してより効率的です。 ただし、同じ数の数量に対して、10進表記が2進表記よりもどれだけ短いかに注意してください。 2進表記で5ビットかかるものは、10進表記で2桁しかかかりません。 これは、さまざまな記数法に関して興味深い質問を提起します。限られた数の暗号位置または場所で、どれだけの数を表すことができるでしょうか。粗ハッシュマークシス

ローマ数字 ローマ人は、さまざまな記号（または暗号）を使用したため、ハッシュマークを大幅に改善したシステムを考案しました。 ）ますます大量を表すため。 1の表記は大文字のIです。5の表記は大文字のVです。他の暗号の値は増加しています： X =10 L =50 C =100 D =500 M =1000 暗号のすぐ右側に同じかそれ以下の値の別の暗号が付随していて、他の暗号の右側に他の暗号よりも大きい暗号がない場合、その他の暗号の値が合計量に追加されます。 したがって、VIIIは数字の8を表し、CLVIIは数字の157を表します。一方、暗号のすぐ左に値の小さい別の暗号が付随して

数値の表現は当たり前のことです。これは、電子工学の研究において良いことでも悪いことでもあります。 電子回路の分析に使用される多くの計算で数値を使用および操作することに慣れているという点で、これは良いことです。 一方、小学校以降に教えられてきた特定の表記法は ではありません。 最新の電子コンピューティングデバイスで内部的に使用されているシステムであり、さまざまな表記法を学習するには、深く根付いた仮定を再検討する必要があります。 数字 まず、数字と数字を表すために使用する記号の違いを区別する必要があります。 番号 は数学的な量であり、通常、電子機器では電圧、電流、抵抗などの物理量と相関

化学元素の周期表。

化学元素の周期表。

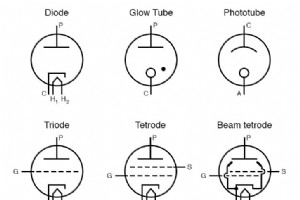
カソード ：これは加熱されて電子を放出する電極です。 アノード ：真空管またはバルブのこの電極は、陰極から電子を引き付ける可能性が高いです。 グリッド ：これは可変電位のバルブ電極であり、カソードとアノードの間の電子の流れを制御するために使用されます。 フィラメント ：最近のほとんどのバルブは間接的に加熱されています。つまり、フィラメントはカソードに接続されていません。フィラメントは陰極を加熱し、陰極は電子を放出します。初期のバルブは直接加熱され、フィラメントを使用して電子を放出しました。ただし、これにより、バルブの使用方法に制限が生じました。間接的に加熱される陰極を使用す

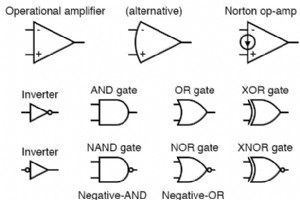
論理ゲートは、デジタル回路の基本的な構成要素として割り当てられています。 論理ゲートは、入力レベルの組み合わせで1つの出力レベルを生成する機能を備えたデバイスと見なされます。 論理ゲートの入力と出力は、HIGHとLOW、TRUEとFALSE、ONとOFF、または単に1と0と呼ばれる2つのレベルにあります。 ANDゲートは、各入力が論理1状態のときに論理1状態の出力を生成し、入力のいずれかが論理0状態にある場合でも論理0状態の出力を生成します。 ANDゲートと同様に、ORゲートにも2つ以上の入力がありますが、出力は1つだけです。 ORゲートは、入力のいずれかが論理1状態の場合でも、論理

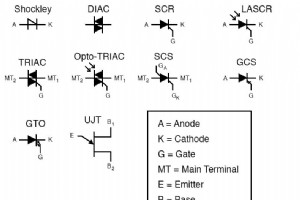
サイリスタは、多くの異常な特性を備えたデバイスです。アノード、カソード、ゲートの3つの端子があり、熱電子バルブ/真空管技術を反映しています。 予想されるように、ゲートは制御端子であり、主電流はアノードとカソードの間を流れます。 DIAC回路記号は、図のように2本の線の間にある2つの三角形から生成されます。 ある意味で、これは2つのジャンクションと見なすこともできるデバイスの構造を示しています。 デバイスの2つの端子は通常、アノード1とアノード2、またはメイン端子1と2、つまりMT1とMT2のいずれかで指定されます。 トライアックを外側から見ると、2つの連続したサイリスタと見なされる場

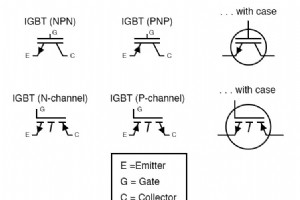
本質的に、IGFETはBJTのベース電流を制御し、BJTはコレクタとエミッタ間の主負荷電流を処理します。このように、非常に高い電流利得がありますが（IGFETの絶縁ゲートは制御回路から実質的に電流を引き出さないため）、完全導通中のコレクタからエミッタへの電圧降下は通常のBJTと同じくらい低くなります。

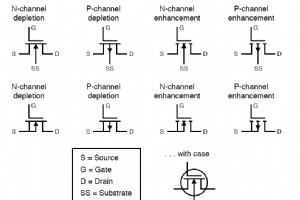
デプレッションモードとエンハンスメントモードのMOSFETの記号があります。破線と実線に注意してください。 空乏モードでは、MOSFETのゲート電圧がソース（S）からドレイン（D）への導電性チャネルを遮断します。 エンハンスメントモードでは、MOSFETのゲート電圧がソースからドレインへの導電性チャネルを開きます。 関連するワークシート： 絶縁ゲート電界効果トランジスタワークシート

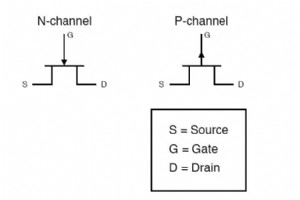
ゲートの矢印の方向は、ゲート接合部が順方向にバイアスされているときにゲート電流が流れる方向を示していることに注意してください。 したがって、NチャネルJFETの場合、ゲート接合部の矢印はデバイスを指し、PチャネルJFETの場合、デバイスから離れています。 関連するワークシート： 接合型電界効果トランジスタ（JFET）ワークシート

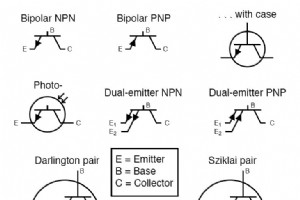
バイポーラトランジスタの回路記号はそれほど多くありません。 もちろん、NPNトランジスタとPNPトランジスタを示すさまざまな回路記号があります。 これに加えて、一部のトランジスタ回路記号には円が付いていますが、そうでないものもあります。 円が含まれていない場合、複数のエミッタや基本トランジスタの他のバリエーションを組み込むのが簡単であるため、ICの内部回路を詳細に説明する回路で広く使用されています。 関連するワークシート： バイポーラ接合トランジスタ（BJT）理論ワークシート TTL論理ゲートワークシート スイッチワークシートとしてのバイポーラ接合トランジスタ オプトエレクト

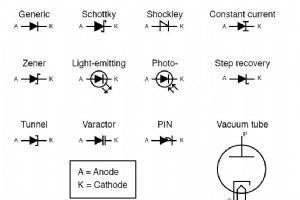
ダイオード は、p-n接合と呼ばれる、P型とN型の半導体材料を組み合わせて作られた電子部品で、両端にリード線が付いています。 これらのリード線を使用すると、ダイオードを電子回路に簡単に組み込むことができます。 n型半導体に接続されたリード線はカソードと呼ばれます。 。したがって、カソードはダイオードのマイナス側です。 ダイオードのプラス側、つまりp型半導体に接続されたリード線はアノードと呼ばれます。 関連するワークシート： オプトエレクトロニクスデバイスワークシート サイリスタワークシート ツェナーダイオードワークシート 特殊ダイオードワークシート 整流ダイオードワークシート

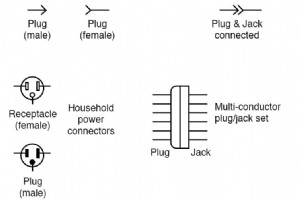
電気コネクタは、電気終端を結合して電気回路を作成するために使用される電気機械装置です。 電気コネクタは、プラグ（オス型）とジャック（メス型）で構成されています。接続は、ポータブル機器の場合のように一時的なものである場合もあれば、組み立てと取り外しのための工具が必要な場合もあります。または、2本のワイヤーまたはデバイス間の永続的な電気的ジョイントとして機能する場合もあります。 アダプターを使用して、異なるコネクターを効果的にまとめることができます。 関連するワークシート： 電気接続ワークシート

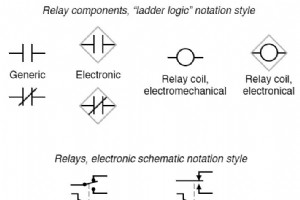
ラダーロジックの背後にある構造は、リレーロジックで使用された電気ラダー図に基づいています。 これらの図は、リレーパネルでデバイス間の接続がどのように行われたかを示しています。これらは、2本の垂直レールとそれらの間にラングがあるラダーに似た方法で構築されているため、「ラダー」図と呼ばれます。 関連するワークシート： 基本的な電磁リレーワークシート