








SPICEは、アナログ電子回路をシミュレートするように設計されたコンピュータープログラムです。その当初の意図は集積回路の開発であり、その名前の由来は S エミュレーション P 私のログラム 統合された C ircuit E mphasis。 SPICEの起源は、CANCERと呼ばれる別の回路シミュレーションプログラムにまでさかのぼります。 U.C.のロナルドローラー教授によって開発されました。バークレーは1960年代後半に彼の学生の何人かと一緒に、CANCERは1970年代初頭まで改善され続けました。 Rohrerがバークレーを離れたとき、CANCERはSPICEに書き直され、名前

「ElectronicsWorkbenchを使用すると、紙の上ですでに使い慣れているものとまったく同じに見える回路回路図を作成できます。さらに、電源スイッチを切り替えて、回路図が実際の回路のように動作するようにすることができます。他の電子シミュレータでは、SPICEノードリストをテキストファイルとして入力する必要がある場合があります。これは、高度な電子エンジニアを除くすべての機能を超える回路の抽象的な表現です。」 —(Electronics Workbenchユーザーガイド—バージョン4、7ページ) この紹介は、 Electronics Workbench と呼ばれる回路シミュレーション

解が数値である通常の方程式とは対照的に、微分方程式は、解が実際に関数であり、その未知の関数の少なくとも1つの導関数が方程式の一部である方程式です。 関数の不定積分を見つける場合と同様に、多くの場合、複数の可能性を含む解が残されます(不定積分に通常見られる定数「c」の多くの可能な値を考慮してください)。微分方程式に答える関数のセットは、その微分方程式の「一般解」と呼ばれます。そのセットのいずれか1つの関数は、その微分方程式の「特定の解」と呼ばれます。微分方程式内の微分と積分の参照変数は、「独立変数」として知られています。
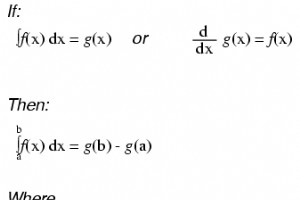
関連ワークシート: 電気回路ワークシートの微積分

一定のルール 数え上げの和則 相違点のルール

注:これはeの非常にユニークで便利なプロパティです。デリバティブの場合のように、そのような関数の不定積分は同じ関数です。不定積分の場合、定数項「c」も末尾に追加されます。

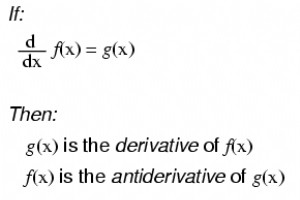
ここで重要なことに注意してください。f(x)の導関数をとると正確にg(x)が得られる場合がありますが、g(x)の不定積分をとっても、必ずしも元の形式のf(x)が得られるとは限りません。例: 定数cは不明であることに注意してください!元の関数f(x)は3x 2 であった可能性があります + 5、3x 2 + 10、3x 2 + 何でも 、およびf(x)の導関数はまだ6xでした。したがって、関数の不定積分を決定することは、関数の導関数を決定することよりも少し確実ではありません。 関連ワークシート: 電気回路ワークシートの微積分

一定のルール 数え上げの和則 違いのルール 積の法則 商の法則 べき乗則 他の機能の機能 関連するワークシート: 電気回路ワークシートの微積分
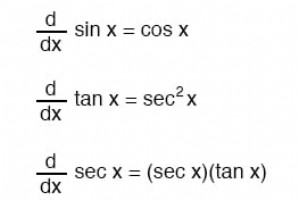
関連するワークシート: 電気回路ワークシートの微積分
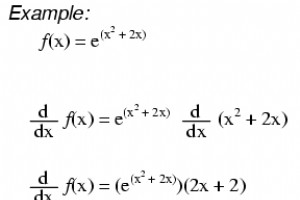
eの導関数の例 比例定数 関係や現象が「指数関数的」であると言うとき、電流、利益、人口などの量は、量が増えるにつれてより急速に増加することを意味します。言い換えると、特定の変数に関する変化率は、その変数の値に比例します。これは、指数関数の導関数が、元の指数関数に定数( k )を掛けたものに等しいことを意味します。 )比例関係を確立します。 $$ \ frac {\ text {d}} {\ text {d} x} a ^ x =ka ^ x $$ 比例定数は、指数の底の自然対数に等しくなります: $$ \ frac {\ text {d}} {\ text {d} x} a ^

関連するワークシート: 電気回路ワークシートの微積分

(「c」は定数です) 関連するワークシート: 電気回路の微積分ワークシート
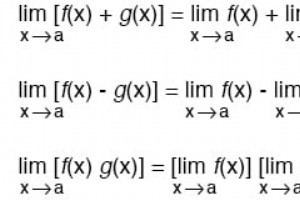
関連するワークシート: 電気回路ワークシートの微積分
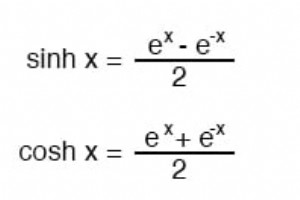
注:すべての角度(x)は、ラジアンの単位で表す必要があります これらの双曲線関数のために。円には2πラジアンがあります(360 o 。

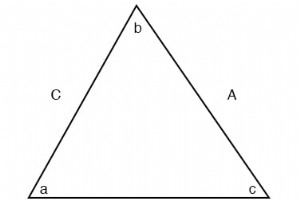
正弦定理(任意の三角形の場合) 余弦定理(任意の三角形の場合)
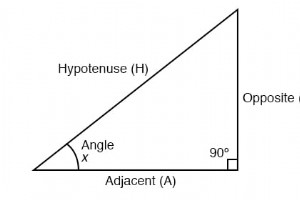
直角三角形 1つの角度が90 o に正確に等しいと定義されます (直角 。 三角関数公式 Hは 斜辺です 、常に直角の反対側にあります。角度xに対して、Oは 反対です。 Aは 隣接です 。 「arcsin」、「arccos」、「arctan」などの「arc」関数は、通常の三角関数を補完するものです。 これらの関数は、比率入力の角度を返します。たとえば、45 o の接線の場合 が1に等しい場合、1の「arctangent」(arctan)は45 o です。 。 「アーク」関数は、辺の長さがわかっている場合に直角三角形の角度を見つけるのに役立ちます。 ピタ

連立方程式と連立方程式とは何ですか? 用語連立方程式 および連立方程式 2つ以上の未知の変数が同数の方程式によって相互に関連している条件を参照してください。 例: この一連の方程式には、 x の値の組み合わせは1つだけです。 および y それは両方を満たすでしょう。 どちらの方程式も、個別に検討すると、有効な(x、y)の無限大があります。 ソリューションですが、一緒に 1つだけです。グラフにプロットすると、この状態が明らかになります: 各線は、実際には可能な x を表す点の連続体です。 および y 各方程式の解のペア。 各方程式には、個別に、無限の数の順序

階乗の定義 記号「!」で示されます 整数の後;その整数と1までのすべての整数の積。 階乗の例: 5! =5 x 4 x 3 x 2 x 1 5! =120 奇妙な階乗 0! =1 1! =1 関連するワークシート: フェーザ数学ワークシート
産業技術