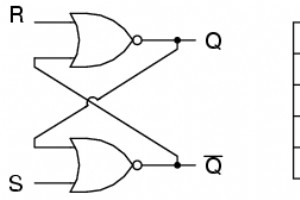
双安定マルチバイブレータには 2つあります 接頭辞 bi で示される安定状態 その名前で。通常、1つの状態は set と呼ばれます もう1つはリセット 。したがって、最も単純な双安定デバイスは、 set-reset として知られています。 、またはS-R、ラッチ。 S-Rラッチを作成するには、次のように、一方の出力がもう一方の入力にフィードバックするように、またはその逆になるように2つのNORゲートを配線できます。 Q出力とnot-Q出力は反対の状態にあると想定されています。 S入力とR入力の両方を1に等しくすると、Qと非Qの両方が0になるため、「想定」と言います。このため、S

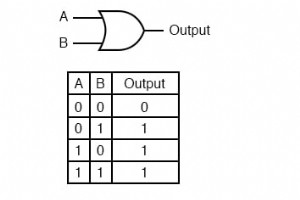
単純なゲートと組み合わせ論理回路を使用すると、任意の入力状態に対して明確な出力状態があります。たとえば、ORゲートの真理値表を見てください。 入力状態の4つの可能な組み合わせ（0-0、0-1、1-0、および1-1）のそれぞれに対して、1つの明確な明確な出力状態があります。カスケード接続された多数のゲートを処理する場合でも、単一のゲートを処理する場合でも、その出力状態は、回路内のゲートの真理値表によって決定されます。 ただし、出力から入力の1つに信号フィードバックを与えるようにこのゲート回路を変更すると、奇妙なことが起こり始めます。 Aが1の場合、出力は必須 同

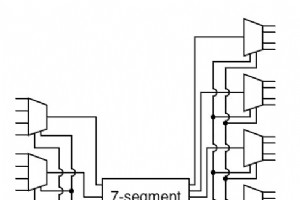
複数の回路を一緒に使用する例として、4桁の数字を表す16個の入力を備えたデバイスを4桁の7セグメントディスプレイに作成しますが、バイナリから7セグメントへのエンコーダを1つだけ使用します。 。 まず、回路の全体的なアーキテクチャは、提供された説明のように見えるものを提供します。 この回路をたどると、上記の説明と一致することを確認できます。表示する桁を選択するために使用される16のプライマリ入力とさらに2つの入力があります。 4桁の7セグメントディスプレイを制御するための28の出力があります。一度にエンコードされるプライマリ入力は4つだけです。ただし、潜在的な質問に気付いたか

マルチプレクサは、muxと略され、複数の入力と1つの出力を持つデバイスです。 マルチプレクサの回路図記号はです。 2対1マルチプレクサの真理値表はです。 I 1 I 0 AD00000010010001111001101011011111 回路の一部として1対2デコーダーを使用すると、この回路を簡単に表現できます。 マルチプレクサは、デマルチプレクサと同じ命名規則で拡張することもできます。 4対1のマルチプレクサ回路は これがマルチプレクサの正式な定義です。非公式には、多くの混乱があります。デマルチプレクサとマルチプ

デマルチプレクサは、dmuxと略されることもあり、1つの入力と複数の出力を持つ回路です。これは、回路が多くのデバイスの1つに信号を送信する場合に使用されます。この説明はデコーダーの説明と似ていますが、デコーダーは多くのデバイスから選択するために使用され、デマルチプレクサーは多くのデバイス間で信号を送信するために使用されます。 デマルチプレクサは、独自の回路図記号を持つほど頻繁に使用されます（下の図） 1対2のデマルチプレクサの真理値表は次のとおりです。 IAD 0 D 1 0000010010101101 回路の一部として1対2デコーダーを使用すると、この

エンコーダーとは何ですか？ エンコーダは、信号のセットをコードに変換する回路です。 1対2のデコーダーの真理値表を逆にして、2対1のラインエンコーダーの真理値表の作成を始めましょう。 D 1 D 0 A010101 この真理値表は少し短いです。完全な真理値表は次のようになります： D 1 D 0 A00 01010111 私たちが答える必要がある1つの質問は、それらの他の入力をどうするかということです。それらを無視しますか？追加のエラー出力を生成させますか？多くの回路では、この問題は、どの入力がアクティブであるかだけでなく、入力がアクティブになった順序も知

デコーダーは、コードを信号のセットに変更する回路です。エンコーディングの逆を行うため、デコーダと呼ばれますが、設計が簡単なため、エンコーダとデコーダを使用したデコーダの研究を開始します。 デコーダーの種類 ラインデコーダー 一般的なタイプのデコーダーは、n桁の2進数を取得し、それを2 n にデコードするラインデコーダーです。 データ行。最も単純なのは1対2のラインデコーダーです。真理値表は次のとおりです。 AD 1 D 0 001110 Aはアドレス、Dはデータラインです。 D 0 はAおよびD 1 ではありません はAです。回路は下の図のようになります。

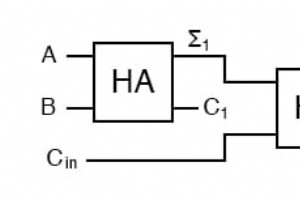
ハーフアダーは、複数の2進数を追加するまで非常に便利です。 2進数の加算器を開発するための遅い方法は、真理値表を作成してそれを減らすことです。次に、3進数の加算器を作成する場合は、もう一度実行します。次に、4桁の加算器を作成する場合は、もう一度実行します。すると...回路は速くなりますが、開発時間は遅くなります。 2進数の合計を見ると、複数の2進数に加算を拡張する必要があることがわかります。 11 11 11 --- 110 中央の列が使用する入力の数を確認します。加算器には3つの入力が必要です。 a、b、および前の合計からのキャリー。2入力加算器を使用して3入力加算器を作成できます。

便利な組み合わせロジックの最初の例として、2桁の2進数を足し合わせることができるデバイスを作成しましょう。答えがどうあるべきかをすばやく計算できます： 0 + 0 =0 0 + 1 =1 1 + 0 =1 1 + 1 =10 2 したがって、2つの入力（aとb）と2つの出力が必要になります。低次の出力は合計を表すためΣと呼ばれ、高次の出力はC out と呼ばれます。 それは実行を表すからです。真理値表は次のとおりです。 ABΣC out 0000011010101101 ブール方程式を単純化するか、カルノー図を作成すると、以下に示す同じ回路が生成されますが、結果を

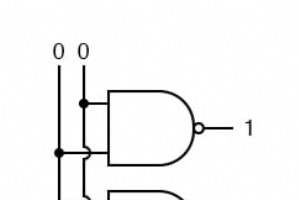
「組み合わせ」という用語は、数学から来ています。数学では、組み合わせは順序付けられていないセットです。これは、アイテムが入った順序を誰も気にしないという正式な方法です。ほとんどのゲームはこのように機能します。一度に1つずつサイコロを振って、2の後に3を付けると次のようになります。 3の後に2を振った場合と同じです。組み合わせロジックを使用すると、入力が変更された順序に関係なく、回路は同じ出力を生成します。 入力がいつ変化するかに依存する回路があり、これらの回路はシーケンシャルロジックと呼ばれます。章のタイトルに「シーケンシャルロジック」という用語はありませんが、次のいくつかの章ではシーケンシ

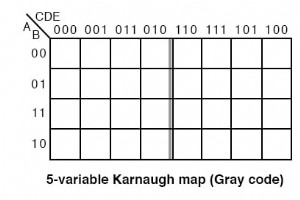
より大きなカルノー図は、より大きな論理設計を減らします。どれくらいの大きさで十分ですか？これは、入力の数、ファンインによって異なります。 、検討中の論理回路に。大規模なプログラマブルロジック企業の1つが答えを持っています。 顧客の設計ライブラリから抽出されたアルテラ独自のデータは、異質性の価値をサポートしています。アルテラは、ロジックコーンを調べ、それらをLUTベースのノードにマッピングし、各ノードで最適な入力の数で並べ替えることにより、ファンインの分布が2〜6の入力間でほぼフラットで、ピークが良好であることを発見しました。 5時。 答えは、ほとんどすべての設計で6入力以下、平均的な論理設計

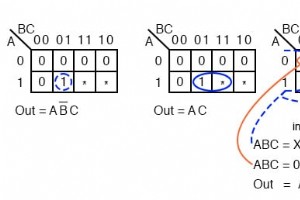
これまで、入力条件が完全に指定された場合の論理削減の問題について検討してきました。つまり、3変数の真理値表またはカルノー図には2 n がありました。 =2 3 または8エントリ、完全なテーブルまたはマップ。 一部の現実の問題については、必ずしも完全な真理値表に記入する必要はありません。表全体に記入しないこともできます。 たとえば、4ビットとしてエンコードされたBCD（Binary Coded Decimal）番号を処理する場合、BCD範囲（0、1、2…9）を超えるコードは気にしない場合があります。 16進数（Ah、Bh、Ch、Eh、Fh）の4ビット2進コードは、有効なBCDコードでは

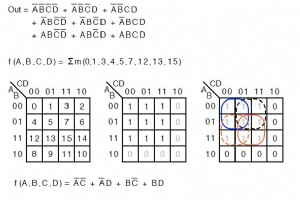
参考までに、このセクションでは、カルノー図に割り当てられたmintermsとmaxtermsを説明するために一部のテキストで使用されている用語を紹介します。それ以外の場合、ここに新しい資料はありません。 Mintermsの用語 Σ（シグマ）は合計を示し、小文字の「m」は最小項を示します。 Σmは最小項の合計を示します。次の例は、私たちのポイントを説明するために再検討されています。単純化されていないロジックのブール方程式の説明の代わりに、mintermsをリストします。 f（A、B、C、D）=Σm（1、2、3、4、5、7、8、9、11、12、13、15） また f（A、B、C、D）=

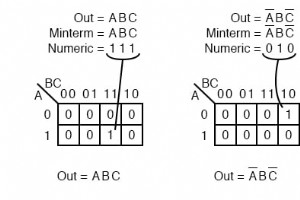
これまで、論理削減の問題に対するSum-Of-Product（SOP）ソリューションを見つけてきました。これらのSOPソリューションのそれぞれについて、Product-Of-Sumsソリューション（POS）もあります。これは、アプリケーションによっては、より便利な場合があります。 Product-Of-Sumsソリューションを使用する前に、いくつかの新しい用語を導入する必要があります。製品用語をマッピングするための以下の手順は、この章にとって目新しいものではありません。 maxtermsの新しい手順と比較するために、mintermsの正式な手順を確立したいだけです。 ミンタ

グレイコードを生成する方法を知っていると、より大きなマップを作成できるはずです。実際に必要なのは、3変数マップの上部にある左から右のシーケンスを見て、4変数マップの左側にコピーすることだけです。以下を参照してください。 4つの変数Kマップの縮小 次の4つの変数カルノー図は、ブール代数には面倒なブール式の削減を示しています。ブール代数を使用して削減を行うことができます。 ただし、特に実行するロジックの削減が多い場合は、カルノー図の方が高速で簡単です。 上記のブール式には7つの積項があります。これらは、上のKマップで上から下および左から右にマップされます。たと

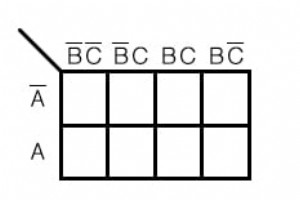
これまでに行った論理単純化の例は、ブール代数を使用してほぼ同じ速さで実行できたはずです。現実世界の論理単純化の問題は、私たちが真剣な仕事をするために、より大きなカルノー図を必要とします。 このセクションでは、いくつかの工夫された例を使用して、実際のアプリケーションのほとんどをCombinatorialLogicの章に残します。考案されたとは、テクニックを説明する例を意味します。 このアプローチでは、CombinatorialLogicの章でより複雑なアプリケーションに移行するために必要なツールを開発します。 カルノー図とグレイコードシーケンス 以前に開発したカルノー図を表示します。右のフ

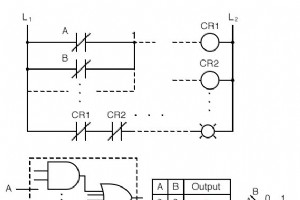
カルノー図を作成したのは誰ですか？ 電気通信エンジニアのモーリス・カルノーは、1953年にベル研究所でデジタルロジックベースの電話交換回路を設計しながらカルノー図を作成しました。 カルノー図の使用 ベン図を使用してカルノー図を作成したので、それを使用してみましょう。カルノー図削減 論理関数は、ブール代数と比較してより迅速かつ簡単に機能します。削減とは、単純化することを意味し、ゲートと入力の数を削減します。 ロジックを最低のコストに簡素化するのが好きです。 コンポーネントを排除することでコストを節約するためのフォーム。最小コストは、ゲートあたりの入力数が最も少ないゲート数が最も少ないと定義

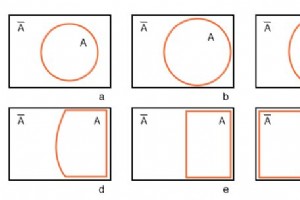
円で始まる A 長方形の A ’ユニバース 下の図（a）では、ベン図をほぼカルノー図に変形しています。 円を拡大します A （b）と（c）で、長方形の A ’ユニバースに準拠します。 （d）で、 A を変更します （e）の長方形に。 A の外に残っているもの は A ’ 。 A ’に長方形を割り当てます （f）で。また、カルノー図ではシェーディングを使用しません。これまでのところ、1変数のカルノー図に似ていますが、ほとんど役に立ちません。複数の変数が必要です。 上の図（a）は、 A を示す前のベン図と同じです。 および A ’ ラベル A を除いて、上記

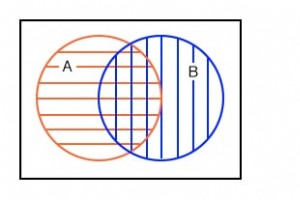
4番目の例には A があります 部分的に重なっている B 。ただし、最初に下のすべてのハッチング領域全体を確認し、次に重複領域のみを確認します。以下に示すように、上の領域にいくつかのブール式を割り当てましょう。 左下には、 A の赤い水平ハッチング領域があります 。 B には青い縦のハッチング領域があります 。 ハッチングのスタイルに関係なく、すべてのハッチングされた領域の合計である両方の領域全体を見ると、右上の図は包括的 OR に対応しています。 A、Bの関数。ブール式は A + B です。 。 これは45 o で示されます ハッチングエリア。ハッチングされた領域の外側はすべ

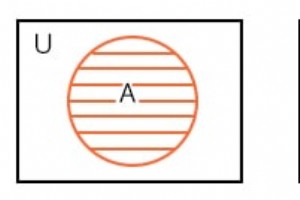
数学者はベン図を使用します セットの論理的な関係を表示する （オブジェクトのコレクション）互いに。おそらく、代数や他の数学の研究でベン図を見たことがあるでしょう。持っている場合は、重なり合った円とユニオンを覚えているかもしれません。 および交差点 セットの。 ベン図の重なり合う円を確認します。デジタルエレクトロニクスで使用される用語であるため、和集合と共通部分の代わりにORとANDという用語を採用します。 ベン図は、前の章のブール代数をカルノー図にブリッジします。ブール代数についてすでに知っていることをベン図に関連付けてから、カルノー図に移行します。 セット 以下に示すように、宇宙から